Markdown + LaTeX
Markdown is a markup language for creating formatted text that is more readable than source code. It can be very useful when you want to include some kind of explanatory text in your project. Check out the PIFOP Markdown cheatsheet.
View and Edit modes
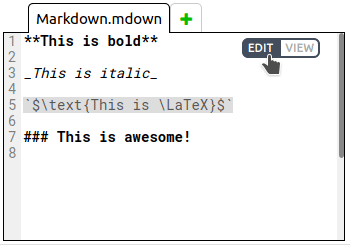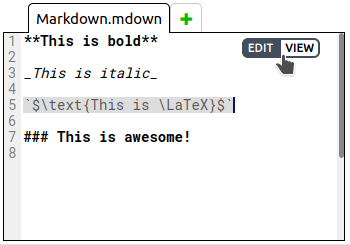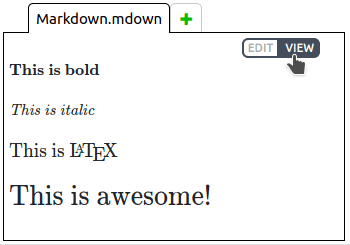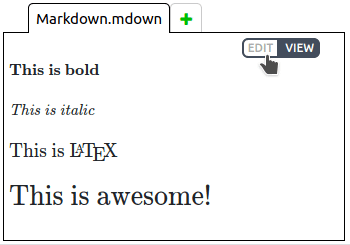
Use the extensions .mdown and .markdown to create markdown files. You can alternate between editing the file source and viewing the formatted markdown by using the buttons in the top left of the text editor, which only appear when a markdown file is open:
LaTeX inline and in blocks
PIFOP markdown interpreter recognizes and formats a subset of LaTeX functions. These functions can be included either inside an inline code span that starts and ends with $, or inside a LATEX code block:
## Markdown + `$\LaTeX$`
Inline `$\LaTeX$` math expression: `$\displaystyle \sum_{(i,j) \in E} x_{ij} = 1$`
```LATEX
\textbf{\LaTeX{} code block with math expression:}\\
\displaystyle \sum_{(i,j) \in E} x_{ij} = 1
```
LaTeX can be used to create files that are full of complex math expressions. Here is a model formulation for the traveling salesman problem:
## TSP formulation
#### Data
- `$V$`: set of vertices `$i \in V$`
- `$n = |V|$`: total number of cities in the salesman region
- `$i = 1$`: city where the salesman lives
- `$E$`: set of arcs `$(i,j)$`, such that `$i \in V$` and `$j \in V$`
- `$c_{ij}: (i,j) \in E$`: distance between cities `$i \in V$` and `$j \in V$`; `$c_{ij}$` may or may not be equal to `$c_{ji}$`.
#### Variables
- `$x_{ij} \in \{0,1\}$`, for all `$(i,j) \in E$`, such that:
- ```LATEX
x_{ij}=
\begin{cases}
1 & \text{if the salesman travels directly from city $i$ to city $j$} \\
0 & \text{otherwise}
\end{cases}
```
- `$y_{ij} \geq 0$`, for all `$(i,j) \in E$`: number of products the salesman has when going from city `$i$` to city `$j$`.
#### Model
```LATEX
\begin{array}{lrcllr}
\text{minimize } & z & = & \displaystyle \sum_{(i,j) \in E} c_{ij}x_{ij} & & (1) \\
\text{subject to} & \displaystyle \sum_{(i,j) \in E} x_{ij} & = & 1 & \forall i \in V & (2) \\
& \displaystyle \sum_{(i,j) \in E} x_{ij} & = & 1 & \forall j \in V & (3) \\
& \displaystyle (n-1) x_{ij} & \geq & y_{ij} & \forall (i,j) \in E & (4) \\
& \displaystyle \sum_{(j,1) \in E} y_{j1} + n & = & \displaystyle \sum_{(1,j) \in E} y_{1j} + 1 & & (5) \\
& \displaystyle \sum_{(j,i) \in E} y_{ji} & = & \displaystyle \sum_{(i,j) \in E} y_{ij} + 1 & \forall (i,j) \in E \lor i \neq 1 & (6) \\
& \displaystyle x_{ij} & \in & \{0,1\} & \forall (i,j) \in E & (7) \\
& \displaystyle y_{ij} & \geq & 0 & \forall (i,j) \in E & (8) \\
\end{array}
```
NOTE: There are limitations on what LaTeX functions are supported. We use KaTeX to interpret LaTeX functions. In order to know whether a function is supported or not, check out the KaTeX list of supported functions.
There are many other things you can do, like create tables and display images. You can learn more about the Markdown + LaTeX syntax in our cheatsheet.